Soundproofing Acoustic transmission

Soundproofing Acoustic transmission in building design refers to processes by which sound energy can be transferred from one part of a building to another. Usually these are:

1. Airborne transmission - a noise source in one room sends air pressure waves which induce vibration to one side of a wall or element of structure setting it moving such that the other face of the wall vibrates in an adjacent room. Structural isolation therefore becomes an important consideration in the acoustic design of buildings. Highly sensitive areas of buildings, for example recording studios, may be almost entirely isolated from the rest of a structure by constructing the studios as effective boxes supported by springs. Air tightness also becomes an important control technique. A tightly sealed door might have reasonable sound reduction properties, but if it is left open only a few millimetres its effectiveness is reduced to practically nothing. The most important acoustic control method is adding mass into the structure, such as a heavy dividing wall, which will usually reduce airborne sound transmission better than a light one.
2. Impact transmission - a noise source in one room results from an impact of an object onto a separating surface, such as a floor and transmits the sound to an adjacent room. A typical example would be the sound of footsteps in a room being heard in a room below. Acoustic control measures usually include attempts to isolate the source of the impact, or cushioning it. For example carpets will perform significantly better than hard floors.
3. Flanking transmission - a complex type of noise transmission, where resultant vibrations from a noise source are transmitted to other rooms of the building usually by elements of structure within the building. For example, in a steel framed building, once the frame itself is set into motion the effective transmission can be pronounced.

Soundproofing and Acoustic Impedance

Sound travels through materials under the influence of sound pressure. Because molecules or atoms of a solid are bound elastically to one another, the excess pressure results in a wave propagating through the solid.

The acoustic impedance (Z) of a material is defined as the product of its density (p) and acoustic velocity (V).

Acoustic impedance is important in

1. the determination of acoustic transmission and reflection at the boundary of two materials having different acoustic impedances.
2. the design of ultrasonic transducers.
3. assessing absorption of sound in a medium.

To calculate the acoustic impedance for any material, its density (p) and acoustic velocity (V) must be known. An increase in the acoustic impedance reduces the amount of acoustic energy that is reflected and transmitted. The values of the reflected and transmitted energy are the fractional amounts of the total energy incident on the interface. Note that the fractional amount of transmitted sound energy plus the fractional amount of reflected sound energy equals one.

Soundproofing Reflection and Transmission Coefficients (Pressure)

Ultrasonic waves are reflected at boundaries where there is a difference in acoustic impedances (Z) of the materials on each side of the boundary. The difference in Z is commonly referred to as the impedance mismatch. The greater the impedance mismatch, the greater the percentage of energy that will be reflected at the interface or boundary between one medium and another.

The fraction of the incident wave intensity that is refracted can be derived because particle velocity and local particle pressures must be continuous across the boundary. When the acoustic impedances of the materials on both sides of the boundary are known, the fraction of the incident wave intensity that is reflected can be calculated with the equation below. The value produced is known as the reflection coefficient. Multiplying the reflection coefficient by 100 gives the amount of energy reflected as a percentage of the original energy.

Since the amount of reflected energy plus the transmitted energy must equal the total amount of incident energy, the transmission coefficient is calculated by simply subtracting the reflection coefficient from one.

Formulations for acoustic reflection and transmission coefficients (pressure) are calculated from direct experimental results. Different materials may be selected and measurements made of their acoustic properties from sensors and transducers the acoustic impedance of one or both materials can then be calculated.

Note that the reflection and transmission coefficients are often expressed in decibels (dB) to allow for large changes in signal strength to be more easily compared. To convert the intensity or power of the wave to dB units, take the log of the reflection or transmission coefficient and multiply this value times 10.

Transducers produce a voltage that is approximately proportionally to the sound pressure. The power carried by a traveling wave is proportional to the square of the pressure amplitude. Therefore, to estimate the signal amplitude change, the log of the reflection or transmission coefficient is multiplied by 10.

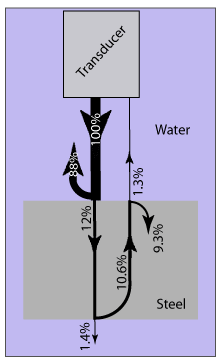
As an example the energy reflected at a water-stainless steel interface is 0.88 or 88%. The amount of energy transmitted into the second material is 0.12 or 12%. The amount of reflection and transmission energy in dB terms are -1.1 dB and -18.2 dB respectively. The negative sign indicates that individually, the amount of reflected and transmitted energy is smaller than the incident energy.

If reflection and transmission at interfaces is viewed through the material, only a small percentage of the original energy makes it back to the transducer, even when loss by attenuation is ignored. For example, consider an immersion inspection of a steel block. The sound energy leaves the transducer, travels through the water, encounters the front surface of the steel, hits the back surface of the steel and reflects back through the front surface on its return to the transducer. At the water steel interface (front surface), 12% of the energy is transmitted. At the back surface, 88% of the 12% that made it through the front surface is reflected. This is 10.6% of the intensity of the initial incident wave. As the wave exits the part back through the front surface, only 12% of 10.6 or 1.3% of the original energy is transmitted back to the transducer.